Medidas de Disperción

 

 

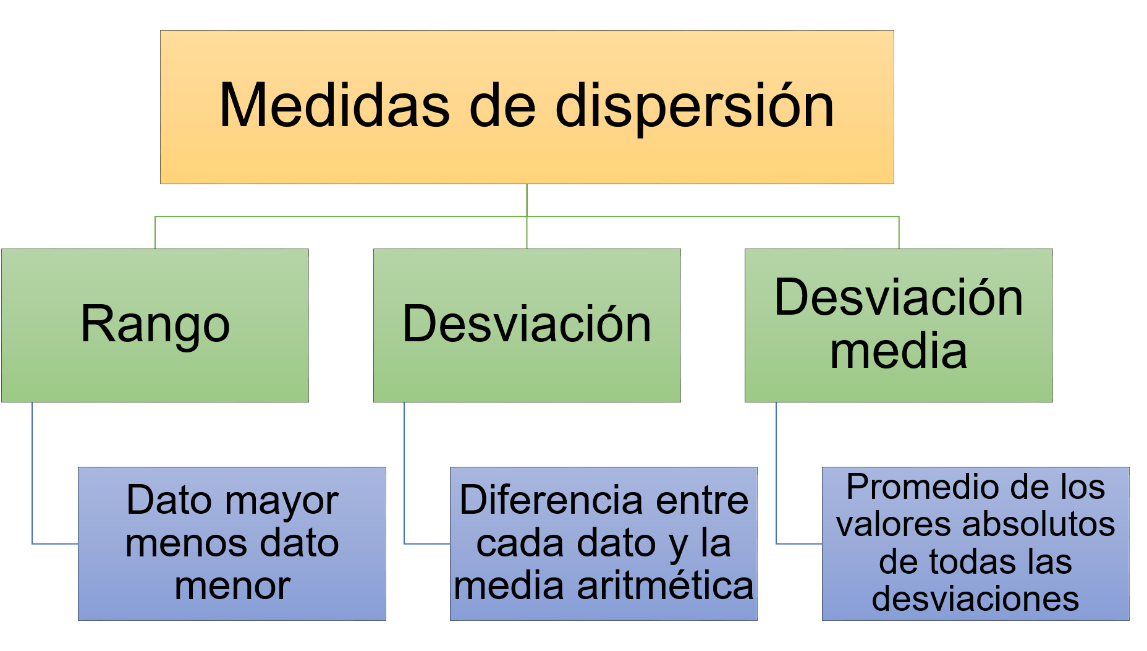
Fig. 12  muestra los datos de las medidas de dispersión.

 

En el análisis estadístico, las medidas de dispersión juegan un papel crucial al proporcionar información sobre la variabilidad de un conjunto de datos. Dos de las medidas más comunes son la varianza y la desviación estándar. Estas medidas son fundamentales para comprender la distribución de los datos y la consistencia de los mismos dentro de un conjunto. En este trabajo, exploraremos en detalle la varianza y la desviación estándar, discutiendo su importancia, fórmulas de cálculo, interpretación y aplicaciones prácticas.

 

Varianza: Definición y Fórmula

La varianza es una medida de dispersión que indica qué tan dispersos están los datos respecto a su media. Matemáticamente, se calcula como la media de los cuadrados de las desviaciones de cada punto de datos respecto a la media del conjunto. Formalmente, la fórmula de la varianza se expresa como:

Fig. 13  muestra los significados de los símbolos de las medidas de dispersión.

Desviación Estándar: Definición y Relación con la Varianza

 

La desviación estándar es simplemente la raíz cuadrada de la varianza y es una medida de dispersión que representa la cantidad promedio de variación o dispersión de un conjunto de datos.

 

Un profesor enseña a dos grandes grupos de introducción al marketing y selecciona aleatoriamente una muestra de calificaciones de los exámenes realizados por los dos grupos. Halle la desviación típica de cada muestra:

·          Grupo 1: 50, 60, 70, 80, 90

·          Grupo 2: 72, 68, 70, 74, 66

Solución 1:

Grupo 1:

De acuerdo a los datos del problema tenemos:

·          Datos = 50, 60, 70, 80, 90

·          Σxᵢ = 350

·          N = 5

·          x̄ = 350/5 = 70,

 

            Vanesa y Jimena Mora, dueñas de una tienda de fotografía, están considerando la posibilidad de invertir en el activo A o en el B. No saben cuál de los dos es mejor y le piden consejo a Sara Nieves, planificadora financiera. Los valores de las tasas de rendimiento de las opciones son:

 Fig. 14  muestra los valores de rendimiento.

¿Cuál es la alternativa más arriesgada?

Solución 2:

Si bien ambas opciones tienen la misma tasa media de rendimiento en los últimos 5 años, es necesario determinar la variabilidad de dicha tasa. Para ello, la desviación estándar es el indicador más frecuente para determinar el riesgo de un activo. En ese caso se calculará la desviación típica para ambas opciones:

Activo A:

De acuerdo a los datos del problema tenemos:

·          Datos = 11.3, 12.5, 13, 12, 12.2     

·          Σxᵢ = 61

·          N = 5

·          x̄ = 61/5 = 12.2

 

La desviación estándar es especialmente útil porque está en las mismas unidades que los datos originales, lo que facilita su interpretación en comparación con la varianza. Desviación estándar (o desviación típica)

La desviación estándar, también llamada desviación típica, es una medida de dispersión estadística. De manera que la desviación estándar es un valor que indica la dispersión de un conjunto de datos estadísticos.

 

La desviación estándar es igual a la raíz cuadrada de la suma de los cuadrados de las desviaciones de la serie de datos partido por el número total de observaciones.

 

Importancia y Interpretación

Tanto la varianza como la desviación estándar proporcionan información crucial sobre la distribución y dispersión de los datos. Una varianza alta indica que los datos están muy dispersos alrededor de la media, mientras que una varianza baja sugiere que los datos están más agrupados cerca de la media. Por otro lado, una desviación estándar grande indica una gran variabilidad en los datos, mientras que una desviación estándar pequeña indica una variabilidad menor.

 

Aplicaciones Prácticas

 

Las medidas de dispersión como la varianza y la desviación estándar tienen numerosas aplicaciones en diversos campos, incluyendo:

 

Finanzas: Para evaluar el riesgo y la volatilidad de inversiones.

Ciencias naturales: En análisis de datos experimentales para medir la precisión de los resultados.

Ingeniería: Para control de calidad y análisis de tolerancia en procesos de fabricación.

Ciencias sociales: En estudios de encuestas y análisis de tendencias.

 

En resumen, la varianza y la desviación estándar son medidas fundamentales de dispersión que proporcionan información valiosa sobre la variabilidad de un conjunto de datos. Su comprensión y aplicación son esenciales en una amplia gama de disciplinas, desde la investigación científica hasta la toma de decisiones en los negocios. Al dominar estas medidas, los analistas pueden obtener una visión más completa y precisa de la distribución de los datos y, por lo tanto, tomar decisiones más informadas.